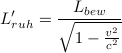Harald Maurer hat geschrieben:Ernst hat geschrieben:Im Gegenteil; ganz richtig. Wiki sagt genau das, was ich gerade erklärte:
Ìn S wird die kontrahierte Länge des sich in S' ruhenden Balls gemessen. Gemäß der angegebenen Formel. Das bedeutet umgekehrt natürlich auch, daß der in S befindlicher Ball in S' eine größere Länge hat. Genau diesen Effekt hatte ich beschrieben.
Aber natürlich hat der Ball in S immer die gleiche Länge. Mit größerer Geschwindigkeit wird seine Länge in S' größer. (Siehe dazu auch Trias Rechnung)
(Was immer man sich beim Ball als Länge vorstellen soll )



Sagen wir mal, in S befindet sich ein Ball und in S' befindet sich auch ein Ball. Beide Bälle haben einen Durchmesser von 30 cm. S und S' bewegen sich zueinander. Im Ruhesystem S wird der in S' befindliche Ball kontrahiert gemessen (weil er in S der bewegte Ball ist). Im Ruhesystem S' wird der in S befindliche Ball kontrahiert gemessen (weil er in S' der bewegte Ball ist). Jeder Beobachter misst daher den im anderen IS befindlichen Ball kontrahiert, in den Ruhesystemen haben die Bälle ihre Eigenlänge (Durchmesser 30 cm). Diese kann jeder Beobachter, welcher den bewegten Ball kontrahiert misst, ermitteln nach der Formel
Was soll Deiner Meinung nach daran falsch sein?
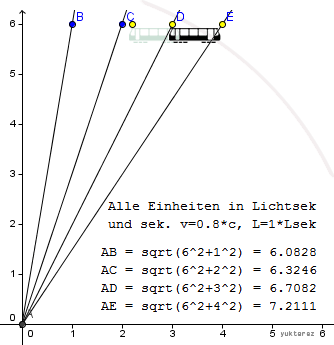
Der zweite Beobachter. Es existiert in unserem Beispiel nur ein Beobachter in S; den Oberleitungswärter. Der in S unbewegte Ball mit 30cm erscheint ihm in S zu 30cm und im S' zu (geschätzt) 45cm. Ein anderer Ball, der in S' mit 30cm vorhanden ist, erscheint in S zu 18cm.
Die Transformation von S nach S' ergibt ja das, was der in S befindliche Beobachter in S' sieht und von dem er glaubt, daß auch der Beobachter in S' identisches sehen müßte. Ein Beobachter in S' sieht aber etwas ganz anderes. Darum die Formeln mit der relativistischen Vertauschung. Jeder sieht was anderes. Der eine glaubt, seine Uhren laufen schneller: der andere wiederum glaubt, seine Uhren laufen schneller.
.
.
.
.