Ernst hat geschrieben:Wie gesagt, ist die Auswertung der Gleichzeitigkeit/Ungleichzeitigkeit nachrangig. Die Frage ist primär: Ist für den Außenbeobachter, der den verkürzten Wagen beobachtet, irgendwann gleichzeitig bei beiden Bügeln kein Kontakt zur Oberleitung vorhanden oder nicht.
Die Antwort ist eindeutig. Wenn der vormals ruhende Wagen mit seiner Länge die Lücke überbrückt, dann tut er es auch gleichzeitig im fahrenden kontrahierten Zustand. Der Wagen ist nämlich für den Außenbeobachter nicht nur kontrahiert, sondern die Uhren im Wagen gehen für den Außenbeobachter erstens auch langsamer und zweitens laufen sie am hinteren Ende gegenüber der Wagenfront vor. Berührt der vordere Bügel gerade das vordere Leitungsende zum Zeitpunkt t, dann ist die Zeit am hinteren Bügel, der ja keine Leitungsberührung hat, bereits t+dt. Aber zum dort früheren Zeitpunkt t hatte er eben noch Kontakt zum hinteren Leitungsende. Zum gleichzeitigen Zeitpunkt t besteht folglich gleichzeitiger Kontakt vorn und hinten.
Das ist nicht richtig. Der Beobachter im Oberleitungssstem (Außenbeobachter) misst mit seinen Maßen und Uhren! Er stellt auch mit seiner Zeit die Berührungszeiten der Kontakte fest! Er misst die Straßenbahn verkürzt und um die Uhren in der Straßenbahn kann er sich nicht kümmern, die sieht er ja auch nicht. Was für ihn gleichzeitig ist (er misst die Straßenbahn gleichzeitig und genau deshalb verkürzt!) ist im IS Straßenbahn nicht gleichzeitig. Das spielt aber in diesem BS keine Rolle, weil hier die Stromabnehmer den Kontakt nie verlieren. Im IS Oberleitung gelten nur die Zeiten und Maße dieses IS. Hier wird nie mit den Uhren des IS Straßenbahn gemessen.
Auch das ist falsch! Das entspräche der Äthertheorie. Wir argumentieren aber mit der SRT! In der SRT gibt es keine c+/-v-Geschwindigkeiten, da gibt es ausschließlich die LG c, die zu keiner Geschwindigkeit hinzugezählt oder subtrahiert werden kann. Und das gilt für jeden Beobachter!
Das muss daher zuerst erklärt sein anhand eines Beispiels: In einer 100 km langen, vor uns
stehenden Straßenbahn (deshalb so lang gewählt, um nicht allzu winzige Zahlen zu erhalten) wird ein Laserstrahl von vorne nach hinten geschickt, wo er z.B. das Bremslicht einschaltet. Nach Einschalten des Lasers leuchtet das Bremslicht daher nach 0,00033356... s auf. Nun lassen wir die Straßenbahn an uns vorbeifahren. Wieder wird der Laser eingeschaltet und das Bremslicht leuchtet auf. Nach welcher Zeit? Natürlich nach derselben Zeit wie vorhin! Das Bremslicht leuchtet nicht deshalb früher auf, weil die Hinterwand dem Laserstrahl entgegenkommt! Wäre das so, so würde der Zeitpunkt des Aufleuchtens eines Bremslichts vom Bewegungszustand abhängen und die Innen-und Außenbeobachter kämen zueinander zu einem Widerspruch. Genau diesen Widerspruch hat Einstein mit der SRT behoben, indem sich die fahrende Straßenbahn verkürzt und die Zeit langsamer in ihr verläuft, was dazu führt, dass die LG in der
bewegten Straßenbahn
auch für den Außenbeobachter c beträgt. Überprüfen wir das mal: Das Licht bewegt sich in der stehenden Straßenbahn mit c, braucht also 0,00033356... s für die Durchquerung. Die kontrahierte Länge einer mit 259000 km/s vorbeifahrenden Straßenbahn beträgt 50,361... km, die dilatierte Zeit für die Durchquerung des Strahls 0,0001679....s. Der Weg durch die Zeit (50,361... / 0,0001679...) = 299792,458 km/s !
Also ob die Straßenbahn steht oder an uns vorbeifährt, die Dauer vom Einschalten des Lasers bis zum Aufleuchten des Bremslichtes verändert sich dadurch nicht. Das ist auch das, was wir beobachten: das künstlich beleuchtete Abteil eines vorbei fahrenden Eisenbahnwaggons bleibt auch für einen Außenbeobachter gleichmäßig ausgeleuchtet. Würde die Vorderwand dem Licht davon - und die Hinterwand dem Licht entgegen laufen, wäre das nicht der Fall. Es sieht so aus, als fahre das Licht mit. Das könnte man mit der Emissionstheorie erklären, die SRT erklärt es mit LK und ZD.
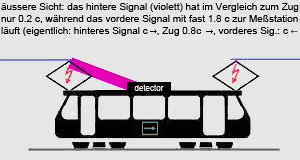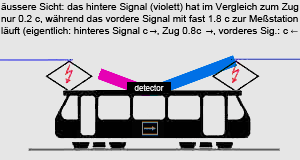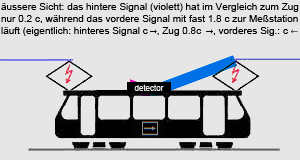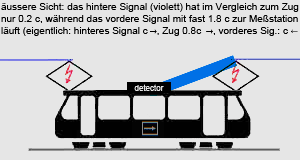
Und deshalb ist dieser Ansatz zur Erklärung des Straßenparadoxons leider falsch:

Hier bewegt sich in der Straßenbahn das rechte Signal mit Überlichtgeschwindigkeit und das linke mit einem Bruchteil von c. Im vorigen Beispiel würden mit diesen Signalen angesteuerte Bremslichter eine seltsame Show bieten. Jeder weiß, dass das nicht der Fall ist!
Lichtsignale oder elektromagnetische Signale in vakuumisolierten Koaxialkabeln bewegen sich lt. SRT also auch in einer
vorbeifahrenden Straßenbahn
für den Außenbeobachter mit "c"! LK und ZD wurden just zur Erklärung dieses Phänomens erfunden. Maxwell reist mit der Straßenbahn gewissermaßen mit! Das muss man berücksichtigen, wenn man Signallaufzeiten in einer vorbeifahrenden Straßenbahn berechnet. Nur in der Äthertheorie würden sich die Signale auf den Äther beziehen und sich die Laufzeiten durch die Bewegung des IS verändern!
Wenn das mal klar gestellt ist, soll nun die m.E. richtige Berechnung der Situation im Oberleitungssystem folgen. Wir modifizieren die Straßenbahn insoferne, dass wir unmittelbar an jeden Stromabnehmerkontakt einen Laser montieren und jeder Laser geradlinig seinen Strahl zur Mitte der Straßenbahn richtet, wo sich ein Detektor befindet, welcher im Moment, an welchem er kein Laserlicht erhält, das Signal zur Bremsung losschickt. Schalten wir die Laser aus, wird nach der mit c zu berechnenden Laufzeit die Bremsung erfolgen. Dieses auf den Laufzeiten beruhende Intervall bis zur Bremsung, ist für jeden Beobachter dasselbe! Das ergibt sich aus der SRT und muss nach dem Relativitätsprinzip auch so sein - andernfalls wäre die Bremsung vom Bewegungszustand und somit vom Bezugssystem abhängig.
(Ruhelänge Straßenbahn 100 km, Straßenbahn bei v=259000 km/s kontrahiert auf 50,361 km
Ruhelänge der Oberleitungslücke 100 km) Genaues Nachrechnen erfordert Berücksichtigung aller Kommastellen.
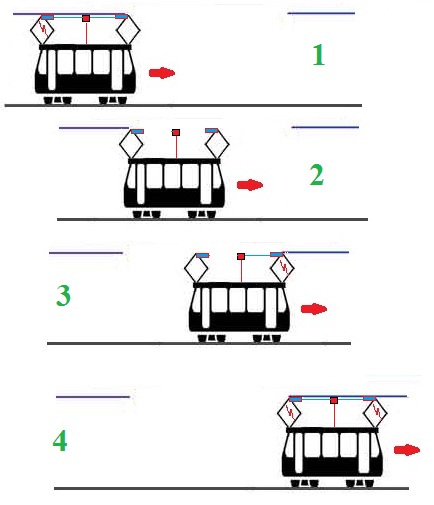
- strassenbahn2.jpg (41.24 KiB) 6803-mal betrachtet
1.) rechter Stromabnehmer fällt ab bei t=0, bewegt sich in 0,0003861... s über die 100 km lange Lücke. Bekommt hier Kontakt. Das Signal bewegt sich nun mit c ( =299792,458 km/s) zur Straßenbahnmitte zurück und braucht dazu 0,0000839931... s. Der Detektor in der Mitte hat daher nach 0,00047... s wieder ein SIgnal. Signallos wurde er nach
0,0000839931... s. Der Detektor ist daher
0,0003861... s lang ohne Signal.
2.) linker Stromabnehmer verliert nach 0,000097222... s den Kontakt. Der Detektor in der Mitte wird signallos nach weiteren 0,0000839931... s, wird also insgesamt ab
0,000181215... s ohne Signal sein. Der linke Stromabnehmer braucht bis zur rechten Oberleitung 0,00048332239... s, das Signal zurück 0,0000839931... s, der Detektor hat also nach 0,0005673155... s wieder ein Signal. Er ist ohne Signal
0,0003861... s lang, dieser Zeitraum ist gleich wie bei 1).
3.) rechter Stromabnehmer: Das Signal verschwindet beim Detektor nach
0,000181215... s und er bleibt
0,0003861... s lang ohne Signal, also bis 0,0005673155... s.
4.) linker Stromabnehmer: Das Signal verschwindet beim Detektor nach
0,000181215..., und er bleibt ohne Signal
0,0003861... s lang, also bis 0,0005673155... s.
Fazit: Das Laserlicht verschwindet an beiden Seiten des Detektors gleichzeitig und trifft danach wieder gleichzeitig an beiden Seiten ein. Inzwischen hat der Detektor 0,0003861... Sekunden lang kein Signal. Er löst daher die Bremsung aus! Im IS Straßenbahn tritt das nicht auf, weil hier stets einer der Abnehmer Kontakt hat!
Damit ist jedenfalls die Annahme widerlegt, dass die Längenkontraktion der SRT eine reale Verkürzung der Straßenbahn wäre! Tatsächlich ist es nur ein Messeffekt. Die Straßenbahn hat immer dieselbe Länge.
q.e.d.
Grüße
Harald Maurer


