Jan hat geschrieben:Und fertig ist.
Fragt sich nur was genau dann fertig ist.
Jan hat geschrieben:Die Wurfparabel ist ein gutes Beispiel und die passende Einleitung dazu habe ich ja jetzt.
Du hast immer noch nicht beantwortet welche Wurfparabel in der EMWW gilt. Zum Vergleich: wenn ich unter Einstein ein Geschoss mit knapp unter c und knapp unter r0=3GM/c² werfe spiraliert es hinein:
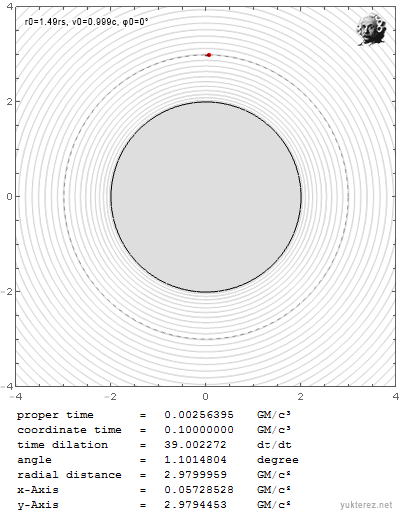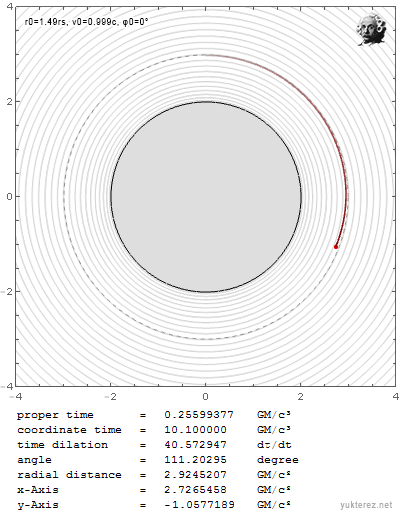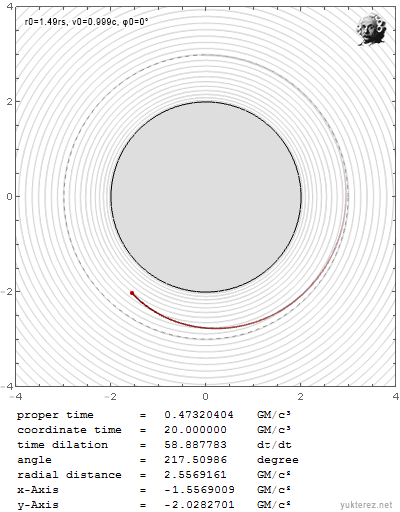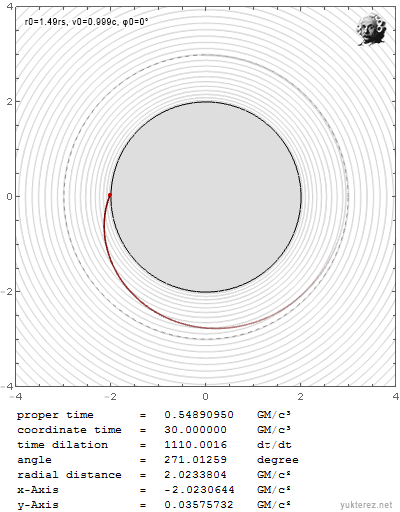
Wenn ich es aber mit der selben Geschwindigkeit knapp über r0=3GM/c² werfe, entkommt es in die Unendlichkeit:
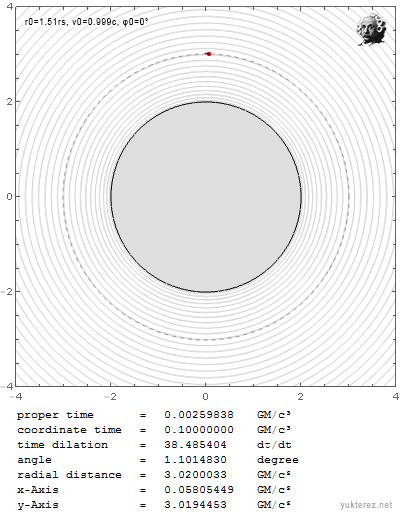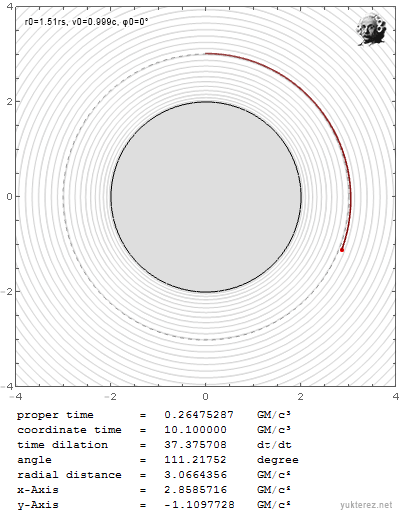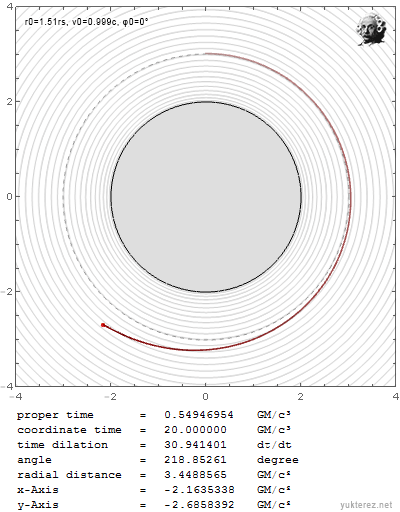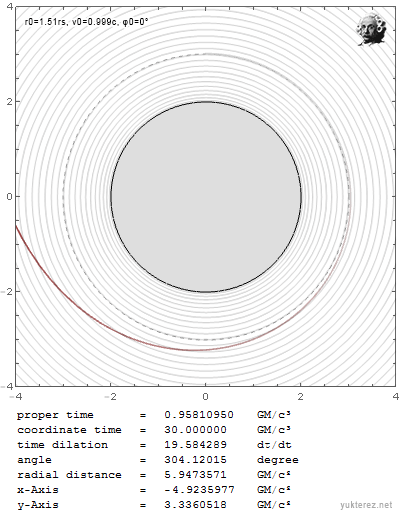
Während es unter Newton in beiden Fällen eine ganz andere Bahn nimmt:
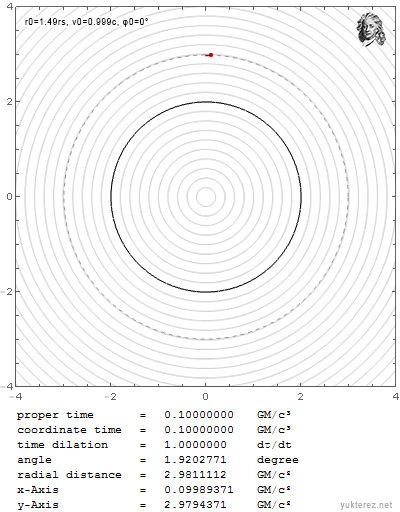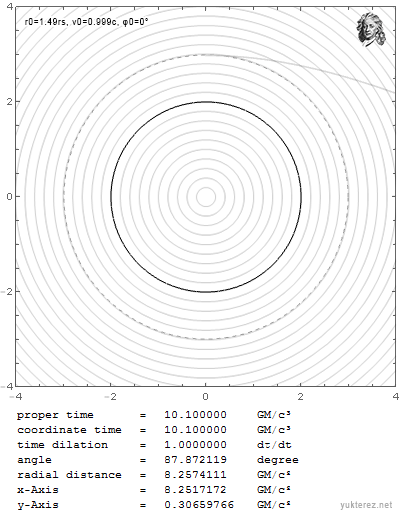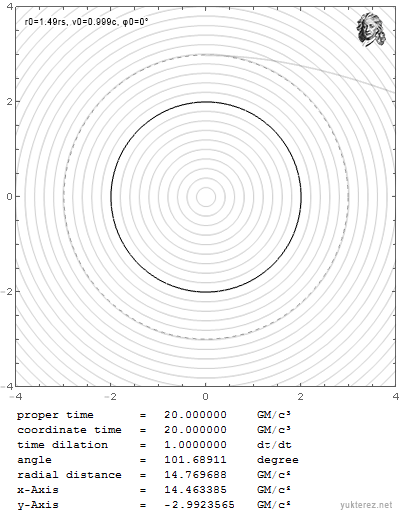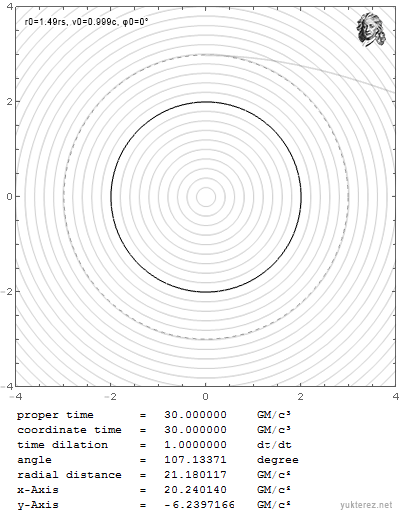
Welche Bahn nimmt es in deiner Theorie? Newton, Einstein, weder noch oder sowohl als auch (im letzteren Falle dürftest du es mit dem Superpositionsprinzip wohl etwas zu weit getrieben haben)? Newton hat keine Periheldrehung - das dürfte den meisten deiner Freunde gefallen. Allerdings hat er auch keine Zentrifugalkraft im Inertialsystem, womit er wiederum im Widerspruch zur kritischen Elite steht. Einstein erklärt die Beobachtungen zwar perfekt, hat aber eine gravitative und geschwindigkeitsabhängige Längenkontraktion, womit du dich in deinen Kreisen auch nicht gerade sehr beliebt machen dürftest. Die meisten Einsteinleugner verwenden wenn sie mit ihrem eigenen Kot auf anständige Leute werfen zum Beispiel gar keine Wurfparabel, weshalb er aber immer auf sie selber zurückfällt. Wofür also entscheidest dich
du?

,
- Code: Alles auswählen
G = 67*^-12; M = 6*^24; c = 3*^8; rs = 2 G M/c^2;
r0 = 151/100 rs; vo = 999/1000 c; φ = Pi/2; vr0 = vo Cos[φ]/j*k; vθ0 = vo/r0 Sin[φ]/j; θ0 = 0; tMax = 2; T = tMax G M/c^3;
d1 = T/10; d2 = d1; wp = 30; step = T/200;
j = Sqrt[1 - vo^2/c^2];
k = Sqrt[1 - rs/r0];
sol = NDSolve[{
r''[t] == -((G M)/r[t]^2) + r[t] θ'[t]^2 - (3 G M)/c^2 θ'[t]^2,
r'[0] == vr0,
r[0] == r0,
θ''[t] == -((2 r'[t] θ'[t])/r[t]),
θ'[0] == vθ0,
θ[0] == θ0,
τ'[t] == Sqrt[c^2 r[t] + r[t] r'[t]^2 - c^2 rs + r[t]^3 θ'[t]^2 - r[t]^2 rs θ'[t]^2]/(c Sqrt[r[t] - rs] Sqrt[1 - rs/r[t]]),
τ[0] == 0
}, {r, θ, τ}, {t, 0, T}, WorkingPrecision -> wp,
MaxSteps -> Infinity, Method -> Automatic,
InterpolationOrder -> All];
t[ξ_] :=
Quiet[χ /.
FindRoot[
Evaluate[τ[χ] /. sol][[1]] - ξ, {χ, 0},
WorkingPrecision -> wp, Method -> Automatic]];
Τ := Quiet[t[ι]];
x[t_] := (Sin[Evaluate[θ[t] /. sol]] Evaluate[r[t] /. sol])[[1]]
y[t_] := (Cos[Evaluate[θ[t] /. sol]] Evaluate[r[t] /. sol])[[1]]
s[text_] := Style[text, FontSize -> font]; font = 11;
Do[Print[
Rasterize[Grid[{{Show[Graphics[{
{Black, Circle[{0, 0}, rs]},
{Lighter[Gray], Dashed, Circle[{0, 0}, r0]}},
Frame -> True, ImageSize -> 400, PlotRange -> 2 r0],
Graphics[{PointSize[0.01], Red, Point[{x[т], y[т]}]}],
ParametricPlot[{x[η], y[η]}, {η, 0, т},
ColorFunction -> Function[{x, y, η},
Hue[0.85, 1, 0.5, Max[Min[(-т + (η + d1))/d1, 1], 0]]],
ColorFunctionScaling -> False],
ParametricPlot[{x[η], y[η]}, {η, 0, т},
ColorFunction -> Function[{x, y, η},
Hue[0, 1, 0.5, Max[Min[(-т + (η + d2))/d2, 1], 0]]],
ColorFunctionScaling -> False]]},
{Grid[{
{" ", s["Eigenzeit"], " = ", s[N[т, 8]], s["sek"]},
{" ", s["Koordinatenzeit"], " = ", s[N[Evaluate[τ[т] /. sol][[1]], 8]], s["sek"]},
{" ", s["Zeitdilatation"], " = ", s[N[Evaluate[τ'[т] /. sol][[1]], 8]], s["dτ/dt"]},
{" ", s["Winkel"], " = ", s[N[Evaluate[(θ[т] /. sol) 180/Pi][[1]], 8]], s["grad"]},
{" ", s["radialer Abstand"], " = ", s[N[Evaluate[r[т] /. sol][[1]], 8]], s["m"]},
{" ", s["x-Achse"], " = ", s[N[x[т], 8]], s["m"]},
{" ", s["y-Achse"], " = ", s[N[y[т], 8]], s["m"]}
}, Alignment -> Left]}}, Alignment -> Left]]
], {т, step, T, step}]
(* yukterez.net, 2016 *)


 ,
, 




 ,
,