Zwillingsparadoxon: Unterschrift-Aktion aus den USA

[fb557ec2107eb1d6]

Wie machst du einen Grenzübergang? Du machst v kleiner und machst den Grenzübergang wo v=0 wird, und schaust welches a und v' du dann hast. das ist doch Standard oder nicht?

Die Begriffe und Operationen Differential, Differentialquotient, Grenzwert und Stetigkeit sind von elementarer Bedeutung für die Physik und speziell für die klassische Mechanik. Die musst du im Schlaf beherrschen, wenn du sinnvoll zum Thema diskutieren willst. Sonst kann es passieren, dass man eine schlechte Figur macht, so wie du jetzt. Eine große Klappe rettet dich da jetzt nicht.

[Hannes]

Hallo Fb 755...... !

Die Begriffe und Operationen Differential, Differentialquotient, Grenzwert und Stetigkeit sind von elementarer Bedeutung für die Physik und speziell für die klassische Mechanik. Die musst du im Schlaf beherrschen, wenn du sinnvoll zum Thema diskutieren willst. Sonst kann es passieren, dass man eine schlechte Figur macht, so wie du jetzt. Eine große Klappe rettet dich da jetzt nicht.

Du vergisst ganz , dass die Diskussion in Mahag gar nicht auf das ausgerichtet ist, was du verlangst.In Mahag soll laut Vorwort Harald Maurers JEDER mitdiskutieren können, der an Physik interessiert ist. Reine Fachdiskussionen gehören wo anders hin.

Mit Gruß
Hannes

[rmw]

Ich muss ihn daher dringend ersuchen, sachlich zu bleiben!

Na ja, da wäre hier wohl eher ein Grund als Moderator einzugreifen: viewtopic.php?f=6&t=353&p=34742#p34742

[Harald Maurer]

Also eigentlich wird es nicht angehalten, denn das Karussell ist ja noch in Bewegung, aber wir schauen so kurz hin, dass man meinen könnte es wäre angehalten.

Wie kurz muss man denn hinschauen, dass man das meinen könnte? Die Rotation ist absolut; entweder gibt es eine Winkelgeschwindigkeit oder es gibt keine. Gibt es eine, können v oder t nicht Null sein.

Selbst Harald Maurer haben sie mit ihrer Verwirrtaktik, oder wie Lothar Pernes gut beschrieben hat, ihrem „Hütchenspiel“ zur Verwirrung gebracht.

Keinesfalls. Aber ein Karussell, das man mathematisch anhält und doch nicht anhält, verwirrt mich schon ein wenig

Du vergisst ganz , dass die Diskussion in Mahag gar nicht auf das ausgerichtet ist, was du verlangst.In Mahag soll laut Vorwort Harald Maurers JEDER mitdiskutieren können, der an Physik interessiert ist. Reine Fachdiskussionen gehören wo anders hin.

Unter den Begriff JEDER fallen wohl Fachleute auch. Aber von einer reinen Fachdiskussion kann hier gar keine Rede sein. Hier wird simples physikalisches Grundwissen behandelt, das jeder haben sollte, wenn er über Physik diskutieren will. Da wäre der richtige Umgang mit Bezugssystemen, Newtons Gesetzen und Definitionen von Kräften die mindeste Voraussetzung. Und nach derzeitigem Paradigma ist eine ursachenlose Kraft, d.h. eine Kraft, die als Ursache keinen Körper hat, der sie ausübt, nun mal eine Scheinkraft. Darüber kommt man auch mit den höchsten mathematischen Purzelbäumen nicht hinweg.

Grüße
Harald Maurer

[contravariant]

Ich habe mehrfach erklärt wie ich es mir denke und habe dem habe ich nichts mehr hinzuzufügen. Insbesondere lasse ich mich nicht auf ein hochtrabendes Mathespielchen ein. Erst recht nicht, wenn man es sich mit drei Pfeilen auch grafisch, fast ohne jegliche Mathe, klar machen kann.

Die Zeichnung gibt halt die Situation nicht korrekt wieder. Die Vektoren v und a sollten denselben Ausgangspunkt haben, d.h. in deiner Zeichnung sollte der Vektor a auch in dem "Blobb" auf der x-Achse anfangen. Dann stehen a und v auch senkrecht aufeinander, was bei eine Kreisbahn korrekt ist.

[Harald Maurer]

Ich habe mehrfach erklärt wie ich es mir denke und habe dem habe ich nichts mehr hinzuzufügen. Insbesondere lasse ich mich nicht auf ein hochtrabendes Mathespielchen ein. Erst recht nicht, wenn man es sich mit drei Pfeilen auch grafisch, fast ohne jegliche Mathe, klar machen kann.

Ja, die drei Pfeife reichen vollends zur Erkenntnis, dass bei v=0 auch der Winkel φ Null wird. Also keine Winkelgeschwindigkeit mehr vorhanden ist. Dann rotiert das Karussell nicht - mit den entsprechenden Konsequenzen.

Grüße
Harald Maurer

[rmw]

Wenn Du Dir die ganz kleine Mühe machen kannst, meine zuletzt angegebenen Links (jeweils nur die aufgerufene Seite) zu lesen,

Das übliche Verwirrspiel ob du es so sehen willst oder nicht: http://books.google.de/books?id=0eTWitU ... em&f=false

Der mitbeschleunigte Beobachter muß demnach schließen dass sie kräftefrei sei. Andererseits weis er dass mit Hilfe des Fadens an der Kugel gezogen wird.

Ich weis nach wie vor nicht wozu es gut sein soll einen Idioten zu definieren der sieht dass an der Schnur gezogen wird und gleichzeitig denkt er sei kräftefrei. Ganz abgesehen davon dass diese Kraft auf ihn selbst ja auch wirkt.
Ich weis wirklich nicht wozu es gut sein soll die Massenträgheitskraft zunächst abzuschaffen und sie dann als "Scheinkraft" wieder einzuführen. Ich denke ich muß dir nicht erklären dass man bei der Berechnung eines beschleunigten Bauteils die Massenträgheitskraft anwenden muß.

Und hier: http://books.google.de/books?id=OGZdSYx ... em&f=false

Diese Kräfte heißen Trägheitskräfte FT. Sie treten nur in beschleunigten beschleunigten Bezugsystemen auf und wirken entgegengesetzt zur Beschleunigung des Systems.

Natürlich treten sie nur in beschleunigten Bezugssystemen auf, in einem IS gibt es ja auch gar keine Beschleunigung.

3. Link: http://www.physik.uni-augsburg.de/did/d ... tel6_1.pdf

Was heißt hier objektive Sichtweise, und warum sollte ein ruhender Beobachter nicht wissen dass der Beschleunigung eine Massenträgheitskraft entgegenwirkt, ist er geistig behindert?

4. Link: http://books.google.de/books?id=DJcRnjN ... em&f=false

Im dynamischen Gleichgewicht verschwindet die Summe aller am Körper angreifenden Kräfte wenn die Trägheitskräfte mit eingeschlossen werden.

Im Prinzip seit Newton bekannt, nur dass es d`Alembert etwas exakter formuliert.

Daran ist nichts was sonderlich schwierig zu verstehen ist. Das ist genau so wie mit der SRT. Man kann an die dortige Vorgangsweise glauben oder sie für Unsinn halten.
Der einzige Grund für einen Beobachter in einem IS die Massenträgheitskräfte abzuschaffen ist die beschleunigte Bewegunng ART konform zu machen.
Dass dieser Unsinn inzwischen in der angewandten Mechanik auch um sich greift wundert mich nicht sonderlich. Es ist ja Generationen von Physikern die SRT ja auch einzureden.

[Harald Maurer]

A) Was an Ihrer Zeichnung qualitativ stimmt ist lediglich, dass die Bahnkurve kreisförmig und der momentane Geschwindigkeitsvektor v tangential an die Bahnkurve steht.

Und noch ein Fehler: v ist unterschiedlich zu v'. Es müsste aber gelten v' = v, denn es ändert sich zwar die Richtung, nicht aber der Betrag.
Richtige Darstellung:

vektoren_v.jpg (18.97 KiB) 6196-mal betrachtet

Grüße
Harald Maurer

[Ernst]

Der einzige Grund für einen Beobachter in einem IS die Massenträgheitskräfte abzuschaffen ist die beschleunigte Bewegunng ART konform zu machen.
Dass dieser Unsinn inzwischen in der angewandten Mechanik auch um sich greift wundert mich nicht sonderlich. Es ist ja Generationen von Physikern die SRT ja auch einzureden.

Entschuldige den Ausdruck, aber das ist Schwachsinn.
Die klassische Mechanik hat mit RT überhaupt nichts zu tun. Sie wird dort nicht mal berücksichtigt Das ist 'ne Manie von Dir.
D'Alembert veröffentlichte das vor über 200 Jahren, und da war von RT nichts zu ahnen.
Daß D'Alembert eine Behandlung im beschleunigten Bezugssystem ist, sieht ein Blinder, jedenfalls wenn er jemals Mechanik studiert hat.
Alle 99% der Quellen werden nach Deiner Meinung von Idioten verfaßt. Da denk mal über die Wahrscheinlichkeit nach, wo man die Idiotie eher finden kann.

Bei der geradlinigen Beschleunigung ist das Prinzip kinderleicht zu erkennen.

Newton
F = m*d²s/dt²
F - m*d²s/dt²=0

Wechselt man in das beschleunigte Bezugssystem, dann kehrt sich die Richtung der Beschleunigung um. Die Kraft bleibt in der gleichen Richtung:

d'Alembert
F - (- m*d²s/dt²) = 0
F + m*d²s/dt² = 0

Da ist nun plötzlich eine Kraft, die in Summe mit F den ausgegleichen Wert Null liefert. Damit beschleunigt sich der Körper nicht mehr. Er bleibt unbeschleunigt, was er ja im beschleunigten Bezugssystem auch ist. Praktisch wird nun die Beschleunigung des beschleunigten Bezugssystems berechnet. Welche selbstverständlich der Beschleunigung der Masse im IS BS entspricht; mit umgekehrten Vorzeichen.
Und diese Kraft, welche im IS BS gar nicht da ist, wird als Schein/Trägheitskraft bezeichent.
Das wird seit mindestens 40 Jahren so gelehrt und angewendet; d'Alembert hats vor 200 Jahren "erfunden".
Da kannst Du die RT noch so hassen, das hat damit überhaupt nichts zu tun.
Vermutlich hattest Du nur den falschen Dozenten.

Gruß
Ernst

[Ernst]

Ich habe mehrfach erklärt wie ich es mir denke und habe dem habe ich nichts mehr hinzuzufügen. Insbesondere lasse ich mich nicht auf ein hochtrabendes Mathespielchen ein. Erst recht nicht, wenn man es sich mit drei Pfeilen auch grafisch, fast ohne jegliche Mathe, klar machen kann.

Lieber Highway,
ich klink mich doch noch mal ein, weil Du so konsequent auf die falschen Propheten setzt.
Verlaß Dich nicht auf die Unwissenden, sondern denke darüber nach, was dir die Ausgebildeten hier nahebringen.

Deine Darstellung ist der richtige Ansatz. Das hatte ich dir ja bereits früher anerkennend bestätigt. Aber Du kommst nicht klar mit der Folgerung.
Zunächst verwirrt Dein Bild, weil Du zu den Geschwindigkeitsvektoren einen Beschleunigungsvektor zeichnest. Der Vektor a muß in dieser Darstellung umbenannt werden in Δv=a*Δt

- Zum Zeitpunkt t=0 beträgt der Geschwindigkeitsvektor v
- Zum Zeitpunkt Δt beträgt der Geschwindigkeitsvektor v'
- In der Zeit Δt wurde der Winkel ϕ = ω*Δt zurückgelegt.
- Der Differnztvektor beider Geschwindigkeitsvektoren beträgt a*Δt

Soweit, so gut. Aber da stimmt noch etwas nicht. v und v' müssen ja den gleichen Betrag haben. Haben sie aber nicht in Deinem Bild. Würdest Du sie gleichgroß einzeichnen, dann würde Δa*t nicht mehr radial liegen. Diese Diskrepanz ist auf die endlich große Zeitspanne für die Betrachtung zurückzuführen.

Zur Ermittlung der wahren Verhältnisse, muß ein Grenzübergang vorgenommen werden. Aber natürlich nicht wie Du meinst, v gegen Null. Das wäre doch idiotisch, da man dann die Scheibe still setzt. Die Grenzwertbetrachtung muß erfolgen für Δt gegen Null, das heißt auch ϕ gegen Null.
Da mußt Du in Deinem Bild keine große Vorstellungskraft aufbringen, wenn Du erkennen willst, daß sich bei kleiner werdendem ϕ der Winkel zwischen a*Δt und v an 90° annähert und infinitesimal schließlich genau 90° wird.
(Komm mir nicht damit, daß bei ϕ=0 dann a*Δt zu Null wird. Dann schick ich Dich uzu einer weiteren Mathevorlesung.
Infinitesimal heißt unendlich klein, aber nicht Null. Es ist ein Grenzübergang)

All das hatte ich ja schon verlinkt gezeigt. Ich behaupte, Du hast es nicht gelesen:

http://www.leifiphysik.de/web_ph11/grundwissen/07kreisbew/vektor2.htm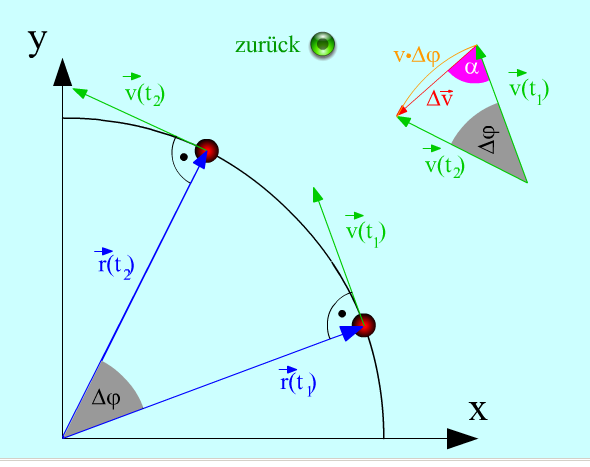

Kreisbewegung Beschleunigung.png

- Der Vektor der Momentanbeschleunigung hat die gleiche Richtung wie der Vektor Δv für den Fall, dass Δt → 0 geht. Dabei ist Δt → 0 gleichbedeutend mit Δφ → 0.
- Die nebenstehende Animation zeigt, welche Richtung Δv hat. Geht in dem Vektordreieck rechts oben der Winkel Δφ → 0, so nähert sich der Winkel α zwischen Δv (und somit a ) und der Momentangeschwindigkeit v dem Winkel 90°.

Fazit:
Der Vektor der Momentanbeschleunigung und der Vektor der Momentangeschwindigkeit stehen aufeinander senkrecht.
Der Vektor a ist antiparallel zum Radiusvektor, er zeigt stets auf den Kreismittelpunkt. Man nennt diese Beschleunigung daher auch Zentripetalbeschleunigung a_r.

Gruß
Ernst