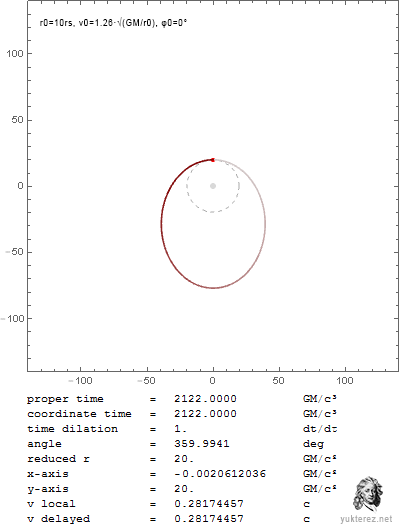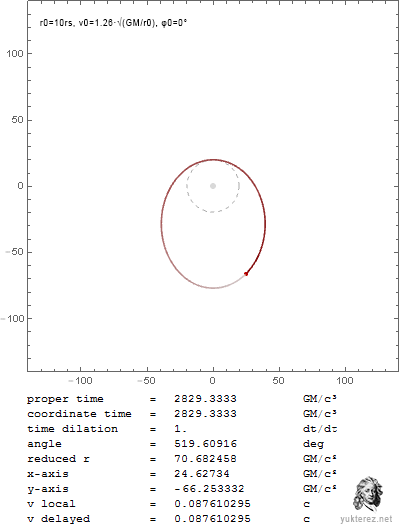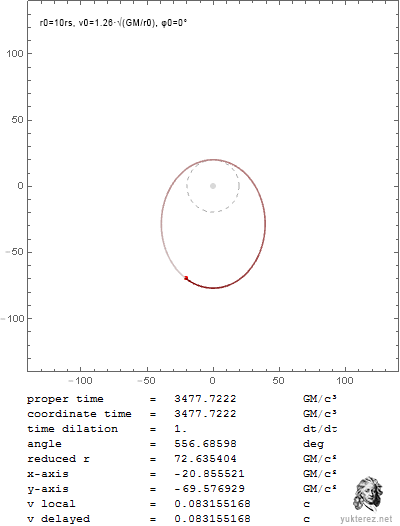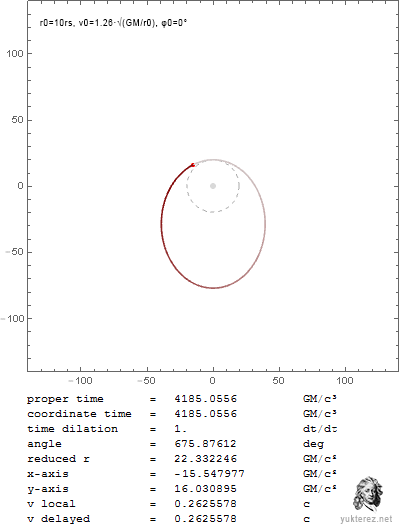
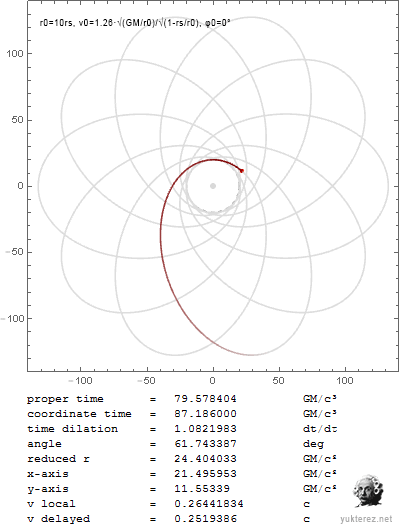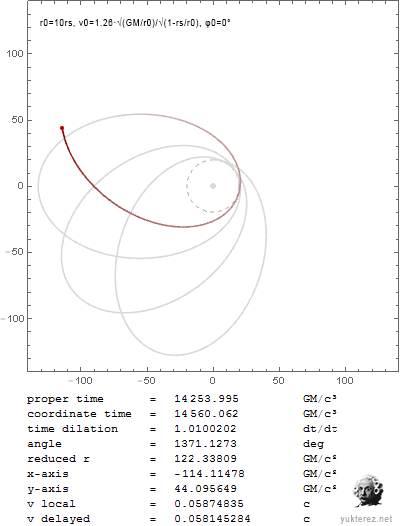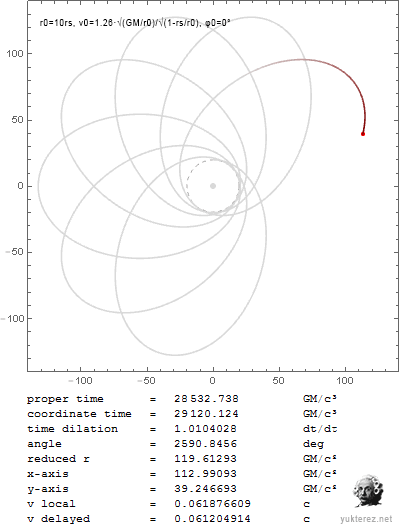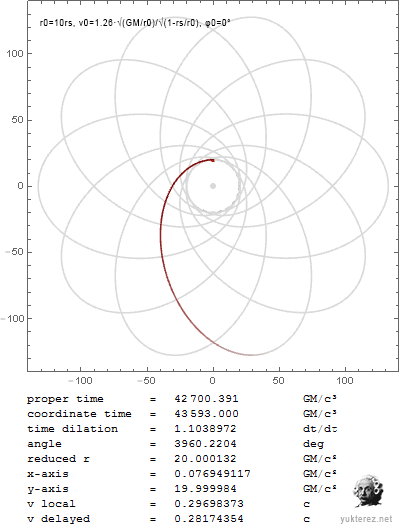
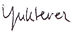Nachdem unsere Relativisten, mit SRT-Avantgardist Yukterez voran, nicht in der Lage sind die partielle Ableitung aus den Originalschriften des Sektenführers zu lösen, habe ich sie selbst gelöst und gezeigt, dass unbewegte Uhren langsamer laufen und damit, dass die SRT nur dummes Zeug und Glaube ist. Wer es nicht glaubt, kann selbst nachrechnen

Und wer weiter glauben und träumen will, soll ein SRT-Jünger werden




Hier sind die Originalgleichungen von Einstein aus seiner
3. Zur Elektrodynamik bewegter Körper § 3. ab Seite 898 Einstein hat geschrieben:Vom Anfangspunkt des Systems k aus werde ein Lichtstrahl zur Zeit
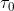
längs der X-Achse nach x’ gesandt und von dort zur Zeit
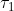
nach dem Koordinatenursprung reflektiert, wo er zur Zeit
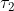
anlange; so muß dann sein:
 = \tau_1)
Einstein hat geschrieben:oder, indem man die Argumente der Funktion
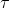
beifügt und das Prinzip der Konstanz der Lichtgeschwindigkeit im ruhenden Systeme anwendet:
 + \tau \left(0,0,0, \left\{ t+\frac{x'}{V - v}+\frac{x'}{V + v} \right\} \right) \right] = \tau \left(x',0,0,t+\frac{x'}{V - v}\right))
Einstein hat geschrieben:Hieraus folgt, wenn man x’ unendlich klein wählt:
 \frac{\partial \tau}{\partial t} = \frac{\partial \tau}{\partial x'} + \frac{1}{V - v} \frac{\partial \tau}{\partial t})
Einstein hat geschrieben:oder
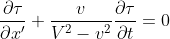
Soweit, so gut.... Wendet man das Prinzip der Konstanz der Lichtgeschwindigkeit im bewegten System k, dann ist es nur logisch zu sagen (und auch zu sehen), dass sich ein Lichtstrahl relativ zum Anfangspunkt vom ruhenden System K mit der Geschwindigkeit V + v bewegt.
Die Gleichungen dazu sehen (laut Einstein) dann so aus:
 + \tau \left(0,0,0, \left\{ t+\frac{x'}{V + v}+\frac{x'}{V - v} \right\} \right) \right] = \tau \left(x',0,0,t+\frac{x'}{V + v}\right))
Wenn man x' unendlich klein wählt:
 \frac{\partial \tau}{\partial t} = \frac{\partial \tau}{\partial x'} + \frac{1}{V + v} \frac{\partial \tau}{\partial t})
oder

(Hier kriege ich [für Bewegung auf X-Achse in Richtung wachsenden x] v^2 -V^2 raus im Nenner und nicht umgekehrt wie Einstein)

Für einen zur Zeit t = 0 in Richtung der wachsenden
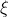
ausgesandten Lichtstrahl gilt:

oder
)
Nun bewegt sich aber der Lichtstrahl relativ zum Anfangspunkt von K (im ruhenden System) gemessen mit der Geschwindigkeit V + v, so daß gilt:

Setzen wir diesen Wert von t in die Gleichung für
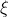
ein, so erhalten wir:
)
Und hier kriege ich wieder das gleiche wie Einstein raus, den Rest der Rechnung kann man sich schenken da wieder gleicher Beta-Faktor hergeleitet wird wie Einstein

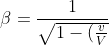^2}})
Damit laufen unbewegte Uhren langsamer, haltet euch also fern von bewegten Gegenstände kann ich euch nur empfehlen