Wurfparabel

[JuRo]

Angenommen, wir beschleunigen Neutronen bis auf c und lassen sie dann auf die Sonne fallen. Werden die dann weiter beschleunigt oder nicht?

Na, du kleiner vollgekoteter Sabber-Lollie? Du bist doch Physiker und Mathematiker mit IQ=150, oder? Also, wie schnell wird ein Testpartikel, wenn man ihm eine Anfangsgeschwindigkeit von v0=0.999c verpasst und ihn dann aus einer Entfernung von r0=100GM/c² auf eine Masse beschleunigen lässt? Wie schnell ist er z.B. nach einer Strecke von 50GM/c², und wie schnell nach 98GM/c²? Du kleiner von oben bis unten angespiebener Alkoholiker (: Komm, mal uns ein paar Lollies, die Zahlen bekommst du sowieso nicht raus (:

Wann beantwortest du endlich mal unsere Fragen, mit deiner vollgeschissener und vollurinierter Unterhose, du Zwangsjackenträger

Wieviel ist V - v, Dummkopf

[Yukterez]

Da von unserem kleinen Braunen sowieso nichts kommen kann zuerst die Ergebnisse für eine zurückgelegte Strecke von 98GM/c²: der Testpartikel der ehemals 0.999c hatte hat wenn er sich in einer Koordinatenentfernung von rs=2GM/c² zum Schwerpunkt befindet, also nach einer Falleigenzeit von 8.90579GM/c³, eine lokale Schalengeschwindigkeit von c, und eine globale Koordinatengeschwindigkeit von 0:


blau: v_lokal, rot: v_global

Die Fakten auf den Tisch knallend,

[JuRo]

Die Fakten auf den Tisch knallend,

Welche Fakten denn

Also, was ist hier Fakt Was sieht man in System k. V oder V - v

PS:
Aufgepasst, keiner von den Relativisten wird die Frage beantworten

[JuRo]

Da von unserem kleinen Braunen...

Was heißt hier unserem

Nur weil du in der Irrenanstalt nicht weißt wie die Welt draussen aussieht, heißt es nicht, dass du vorher (vor deiner Einlieferung) es gewusst haben gekonnt hättest

[Yukterez]

Da die Funktion der Lokalgeschwindigkeit (blau) im Vergleich zur Koordinatengeschwindigkeit (rot) am Plot auf der letzten Seite nicht wirklich zur Geltung kommt hier die beiden Geschwindigkeiten im Verleich. Das Beispiel ist immer noch:

Wie schnell wird ein Testpartikel, wenn man ihm eine Anfangsgeschwindigkeit von v0=0.999c verpasst und ihn dann aus einer Entfernung von r0=100GM/c² auf eine Masse beschleunigen lässt?

Wie man sieht konvergiert die lokale Geschwindigkeit auf c zu, und die Koordinatengeschwindigkeit auf 0:



Getrennt betrachtend,

[JuRo]

Und wieviel ist Einstein's V - v

[Yukterez]

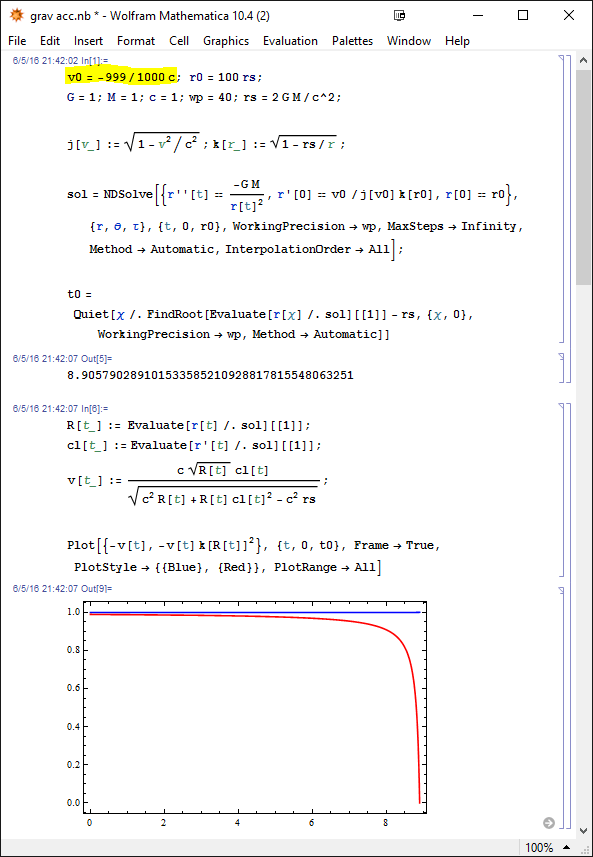
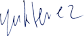Jetzt das Gleiche in die andere Richtung:

Zur Abwechslung platzieren wir einen Beobachter auf der Schale und lassen ihn einen Testpartikel mit nach oben werfen.
Auf jeder Schale haben wir einen Notar sitzen der wenn der Partikel bei ihm vorbeikommt dessen Eigenzeit und Relativgeschwindigkeit misst (links, gelb).
Wir selbst betrachten die Szene aus sicherer Entfernung, und notieren unsererseits wann der Partikel mit welcher Geschwindigkeit bei welcher Schale vorbeifliegt (rechts, grün).

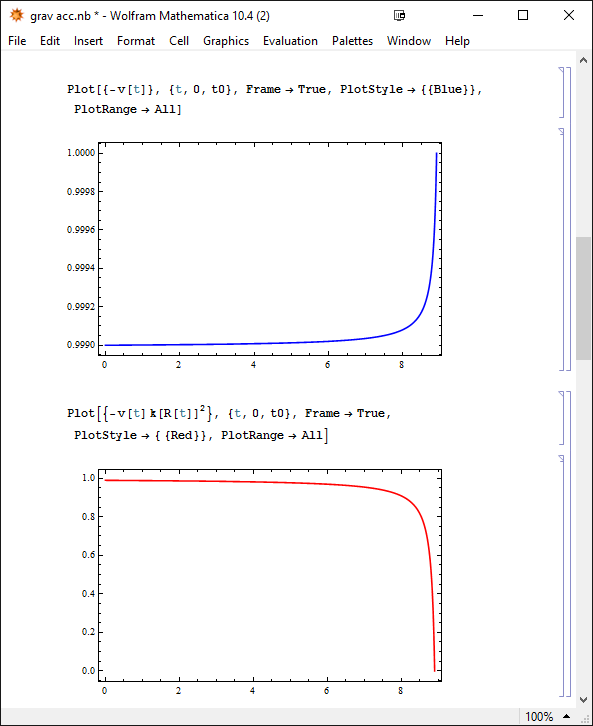
Obwohl es im rechten Bild so aussieht als hätte der Partikel einen Raketenantrieb mit dem er beschleunigt, wird er, obwohl seine Koordinatengeschwindigkeit schneller wird, von der Schwerkraft gebremst. Da die Zeitdilatation aber umso geringer wird je weiter er sich vom Zentrum entfernt, während er auch wenn er auf seinem Weg viel kinetische Energie verliert dennoch fast seine ganze Geschwindigkeit behalten kann, wird er in unserem System tatsächlich schneller, während er lokal langsamer wird.

Das kommt daher weil man den Verlust an Energie im Gravitationsfeld mit Kraft mal Weg erhält, während die kinetische Energie eines Partikels nahe der Lichtgeschwindigkeit fast unendlich ist und daher die Eigengeschwindigkeit kaum langsamer, und daher die Koordinatengeschwindigkeit sogar schneller werden kann (hier ca. um den Faktor 27):



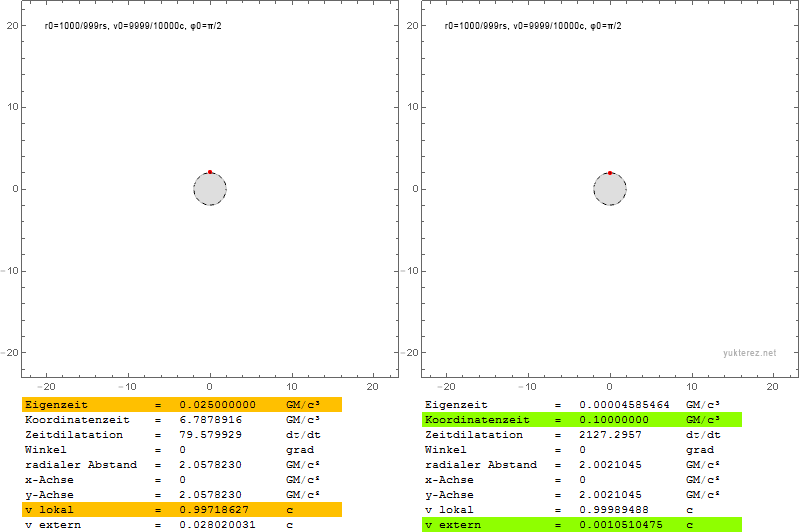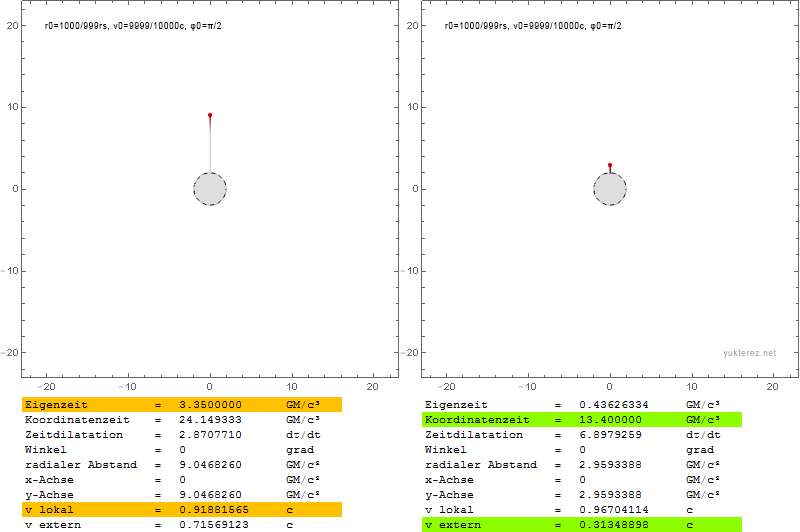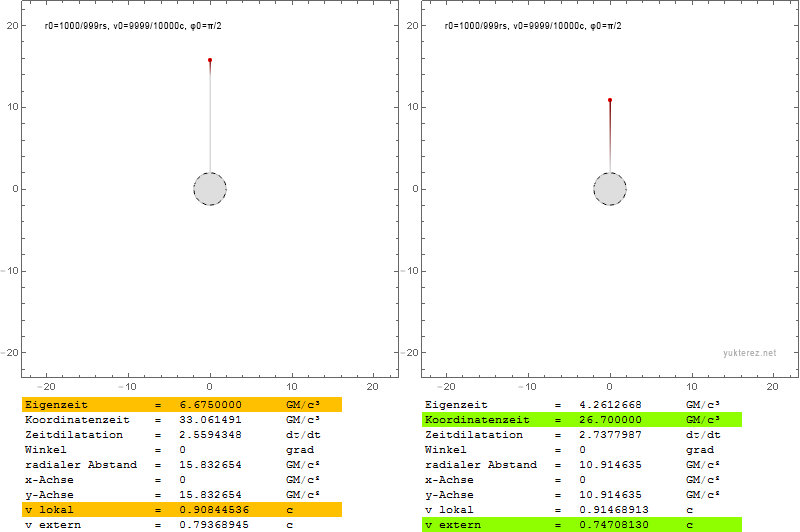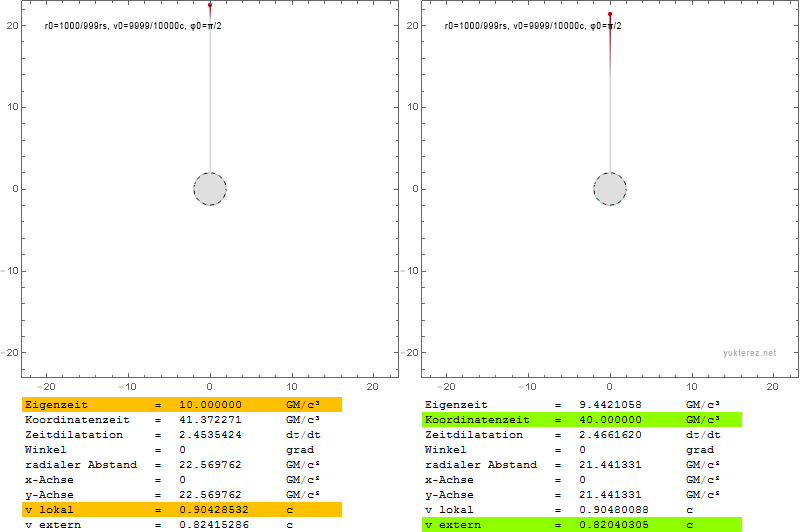
Wir stellen fest dass der Partikel mit 0.03162c geworfen wird, und innerhalb der Zeitspanne von 40GM/c³ auf 0.82040305c beschleunigt.
Bis dahin hat er sich bis zur Schale auf der Koordinate 21.4413GM/c² vorgekämpft.

Die Notare auf den Schalen notieren stattdessen dass der Partikel mit 0.9999c geworfen wird, und wenn er bei der Schale auf 21.4413GM/c² ankommt auf 0.86157c entschleunigt hat.

Unter Newton hätte er in beiden Systemen nach 40GM/c³ Zeit auf 0.31933c entschleunigt und wäre dabei bis zur Schale bei der Koordinate 19.7682GM/c² gekommen.

Von einem System ins andere transformierend,



Edit: Newton hinzugefügt

[Yukterez]

Update: (Edit: bei jedem größeren Update erfolgt auch hier ein Update)

Code: Alles auswählen

ClearAll["Global`*"]

mt1={"StiffnessSwitching", Method-> {"ExplicitRungeKutta", Automatic}};
mt2={"EventLocator", "Event"-> (r[t]-1000001/1000000 rA)};
mt3={"ImplicitRungeKutta", "DifferenceOrder"-> 20};
mt4={"EquationSimplification"-> "Residual"};
mt0=Automatic;
mta=mt0;

A=a;                                   (* pseudosphärisch [BL]: A=0, kartesisch [KS]: A=a *)

wp=MachinePrecision;

tmax=300;                                                                    (* Eigenzeit *)
Tmax=100;                                                              (* Koordinatenzeit *)

r0=7;                                                                      (* Startradius *)
θ0=π/2;                                                                    (* Breitengrad *)
φ0=0;                                                                       (* Längengrad *)
a=9/10;                                                                  (* Spinparameter *)
μ=-1;                                                        (* Baryon: μ=-1, Photon: μ=0 *)

v0=4/10;                                                        (* Anfangsgeschwindigkeit *)
α0=0;                                                        (* vertikaler Abschusswinkel *)
ψ0=ArcTan[5/6];                                                 (* Bahninklinationswinkel *)

vr0=v0 Sin[α0];                                     (* radiale Geschwindigkeitskomponente *)
vφ0=v0 Cos[α0] Sin[ψ0];                      (* longitudinale  Geschwindigkeitskomponente *)
vθ0=v0 Cos[α0] Cos[ψ0];                        (* latitudinale Geschwindigkeitskomponente *)

ε=Sqrt[δ Ξ/((a^2+r0^2)^2-a^2 δ Sin[θ0]^2)]/j[v0]+Lz щ;
Lz=vφ0 Sqrt[Ы^2/j[v0]^2];
pθ0=vθ0 Sqrt[(Ы^2+z0^2)/j[v0]^2];
pr0=vr0 Sqrt[(Ξ/δ)/j[v0]^2];                         (* Energie und Drehimpulskomponenten *)

x0=Sqrt[r0^2+a^2] Sin[θ0] Cos[φ0];
y0=Sqrt[r0^2+a^2] Sin[θ0] Sin[φ0];
z0=r0 Cos[θ0];                                          (* kartesische Anfangskoordinaten *)

j[v_]:=Sqrt[1+μ v^2];                                                    (* Lorentzfaktor *)
щ=2r0 a/((r0^2+a^2)^2-a^2 (r0^2+a^2-2 r0)Sin[θ0]^2);                        (* Frame Drag *)
я=Sqrt[((r[τ]^2+a^2)^2-a^2 Δ Sin[θ[τ]]^2)/(r[τ]^2 +a^2 Cos[θ[τ]]^2)]Sin[θ[τ]];
яi[τ_]:=Sqrt[((R[τ]^2+a^2)^2-a^2 Δi[τ] Sin[Θ[τ]]^2)/(R[τ]^2 +a^2 Cos[Θ[τ]]^2)]Sin[Θ[τ]];
Ы=Sqrt[((r0^2+a^2)^2-a^2 δ Sin[θ0]^2)/(r0^2 +a^2 Cos[θ0]^2)]Sin[θ0];
Σ=r[τ]^2+a^2 Cos[θ[τ]]^2;                                       (* zusammengefasste Terme *)
Σi[τ_]:=R[τ]^2+a^2 Cos[Θ[τ]]^2;
Ξ=r0^2+a^2 Cos[θ0]^2;
Δ=r[τ]^2-2r[τ]+a^2;
Δi[τ_]:=R[τ]^2-2R[τ]+a^2;
δ=r0^2-2r0+a^2;
Щ=Lz^2 Cot[θ[τ]]^2;
Q=pθ0^2+(Lz^2 Csc[θ0]^2-a^2 (ε^2+μ)) Cos[θ0]^2;                       (* Carter Konstante *)
k=Q+Lz^2+a^2 (ε^2+μ);                                                 (* Carter k *)

т[τ_]:=Evaluate[t[τ]/.sol][[1]];                        (* Koordinatenzeit nach Eigenzeit *)
д[ξ_] :=Quiet[Ξ /.FindRoot[т[Ξ]-ξ, {Ξ, 0}]];            (* Eigenzeit nach Koordinatenzeit *)
T :=Quiet[д[tk]];                           

ю[τ_]:=Evaluate[t'[τ]/.sol][[1]];
γ[τ_]:=If[μ==0, "Infinity", ю[τ]];                                           (* totale ZD *)
R[τ_]:=Evaluate[r[τ]/.sol][[1]];                                (* Boyer-Lindquist Radius *)
Φ[τ_]:=Evaluate[φ[τ]/.sol][[1]];                               
Θ[τ_]:=Evaluate[θ[τ]/.sol][[1]];
ß[τ_]:=Sqrt[X'[τ]^2+Y'[τ]^2+Z'[τ]^2 ]/ю[τ];
ς[τ_]:=Sqrt[((a^2+R[τ]^2)^2-a^2 (a^2+(R[τ]-2)R[τ])Sin[Θ[τ]]^2)/((a^2+
       (R[τ]-2)R[τ])(a^2 Cos[Θ[τ]]^2+R[τ]^2))];                         (* gravitative ZD *)
Λ[τ_]:=R[τ]^2+a^2-2 R[τ];
Υ[τ_]:=(R[τ]^2+a^2)^2-a^2 Λ[τ]Sin[Θ[τ]]^2;
ρ[τ_]:=R[τ]^2+a^2 Cos[Θ[τ]]^2;
ω[τ_]:=2R[τ] a/Υ[τ];                              (* Frame Dragging Winkelgeschwindigkeit *)
Ω[τ_]:=ω[τ] Sqrt[X[τ]^2+Y[τ]^2];            (* Frame Dragging beobachtete Geschwindigkeit *)
й[τ_]:=ω[τ] яi[τ] ς[τ];                          (* Frame Dragging lokale Geschwindigkeit *)
ж[τ_]:=Sqrt[ς[τ]^2-1]/ς[τ];                                      (* Fluchtgeschwindigkeit *)
v[τ_]:=If[μ==0, 1, Abs[Re[-((\[Sqrt](-a^4(ε-Lz ω[τ])^2-2 a^2R[τ]^2 (ε-Lz ω[τ])^2-
       R[τ]^4(ε-Lz ω[τ])^2+Δi[τ](Σi[τ]+a^2 Sin[Θ[τ]]^2 (ε-
       Lz ω[τ])^2)))/(Sqrt[-(a^2+R[τ]^2)^2+
       a^2 Sin[Θ[τ]]^2 Δi[τ]](ε - Lz ω[τ])))]]];          (* lokale Dreiergeschwindigkeit *)
pΘ[τ_]:=Evaluate[pθ[τ] /. sol][[1]];
pR[τ_]:=Evaluate[pr[τ] /. sol][[1]];
sh[τ_]:=Sqrt[ß[τ]^2-Ω[τ]^2];
epot[τ_]:=ε-1-ekin[τ];                                             (* potentielle Energie *)
ekin[τ_]:=If[μ==0, ς[τ], 1/Sqrt[1-v[τ]^2]-1];                       (* kinetische Energie *)

dp= \!\(\*SuperscriptBox[\(Y\),\(Y\)]\); n0[z_]:=Chop[N[z]];
                                         
DGL={
t'[τ]==ε+(2r[τ](r[τ]^2+a^2)ε-2 a r[τ] Lz)/(Σ Δ),
t[0]==0,
r'[τ]==(pr[τ] Δ)/Σ,
r[0]==r0,
θ'[τ]==pθ[τ]/Σ,
θ[0]==θ0,
φ'[τ]==(2 a r[τ] ε+(Σ-2r[τ])Lz Csc[θ[τ]]^2)/(Σ Δ),
φ[0]==φ0,
pr'[τ]==1/(Σ Δ) (((r[τ]^2+a^2)μ-k)(r[τ]-1)+r[τ] Δ μ+2r[τ](r[τ]^2+a^2) ε^2-2 a ε Lz)-(2pr[τ]^2 (r[τ]-1))/Σ,
pr[0]==pr0,
pθ'[τ]==(Sin[θ[τ]]Cos[θ[τ]])/Σ (Lz^2/Sin[θ[τ]]^4-a^2 (ε^2+μ)),
pθ[0]==pθ0
};                                                               (* Differentialgleichung *)

sol=NDSolve[DGL, {t, r, θ, φ, pr, pθ, ν}, {τ, 0, tmax},
WorkingPrecision-> wp,
MaxSteps-> Infinity,
Method-> mta,
InterpolationOrder-> All];                                                  (* Integrator *)

X[τ_]:=Evaluate[Sqrt[r[τ]^2+a^2] Sin[θ[τ]] Cos[φ[τ]]/.sol][[1]];
Y[τ_]:=Evaluate[Sqrt[r[τ]^2+a^2] Sin[θ[τ]] Sin[φ[τ]]/.sol][[1]];
Z[τ_]:=Evaluate[r[τ] Cos[θ[τ]]/.sol][[1]];

XYZ[τ_]:=Sqrt[X[τ]^2+Y[τ]^2+Z[τ]^2]; XY[τ_]:=Sqrt[X[τ]^2+Y[τ]^2];  (* kartesischer Radius *)

Xyz[{x_, y_, z_}, α_]:={x Cos[α]-y Sin[α], x Sin[α]+y Cos[α], z};
xYz[{x_, y_, z_}, β_]:={x Cos[β]+z Sin[β], y, z Cos[β]-x Sin[β]};
xyZ[{x_, y_, z_}, ψ_]:={x, y Cos[ψ]-z Sin[ψ], y Sin[ψ]+z Cos[ψ]};

rE=1+Sqrt[1-a^2 Cos[θ]^2];                                           (* äußere Ergosphäre *)
RE[A_]:=
{Sqrt[rE^2+A^2] Sin[θ]Cos[φ], Sqrt[rE^2+A^2] Sin[θ]Sin[φ], rE Cos[θ]};
rG=1-Sqrt[1-a^2 Cos[θ]^2];                                           (* innere Ergosphäre *)
RG[A_]:=
{Sqrt[rG^2+A^2] Sin[θ]Cos[φ], Sqrt[rG^2+A^2] Sin[θ]Sin[φ], rG Cos[θ]};
rA=1+Sqrt[1-a^2];                                                     (* äußerer Horizont *)
RA[A_]:=
{Sqrt[rA^2+A^2] Sin[θ]Cos[φ], Sqrt[rA^2+A^2] Sin[θ]Sin[φ], rA Cos[θ]};
rI=1-Sqrt[1-a^2];                                                     (* innerer Horizont *)
RI[A_]:=
{Sqrt[rI+A^2] Sin[θ]Cos[φ], Sqrt[rI+A^2] Sin[θ]Sin[φ], rI Cos[θ]};

horizons[A_, mesh_]:=Show[
ParametricPlot3D[RE[A], {φ, 0, 2π}, {θ, 0, π},
Mesh->mesh, PlotStyle->Directive[Blue, Opacity[0.15]]],
ParametricPlot3D[RA[A], {φ, 0, 2π}, {θ, 0, π},
Mesh->None, PlotStyle->Directive[Cyan, Opacity[0.15]]],
ParametricPlot3D[RI[A], {φ, 0, 2π}, {θ, 0, π},
Mesh->None, PlotStyle->Directive[Red, Opacity[0.25]]],
ParametricPlot3D[RG[A], {φ, 0, 2π}, {θ, 0, π},
Mesh->None, PlotStyle->Directive[Red, Opacity[0.35]]]];
BLKS:=Grid[{{horizons[a, 35], horizons[0, 35]}}];

                     (* Plot nach Koordinatenzeit *)

display[T_]:=Grid[{
{s[" t coord"], " = ", s[n0[tk]], s["GM/c³"], s[dp]},
{If[μ==0, s[" affineP"], s[" τ propr"]], " = ", s[n0[T]], s["GM/c³"], s[dp]},
{s[" γ total"], " = ", s[n0[γ[T]]], s["dt/dτ"], s[dp]},
{s[" ς gravt"], " = ", s[n0[ς[T]]], s["dt/dτ"], s[dp]},
{s[" r coord"], " = ", s[n0[R[T]]], s["GM/c²"], s[dp]},
{s[" φ longd"], " = ", s[n0[Φ[T]]], s["rad"], s[dp]},
{s[" θ lattd"], " = ", s[n0[Θ[T]]], s["rad"], s[dp]},
{s[" r'τ.Σ/Δ"], " = ", s[N[R'[T] Σi[T]/Δi[T]]], s["mc"], s[dp]},
{s[" φ'τ*rgy"], " = ", s[n0[Φ'[T] яi[T]]], s["mc"], s[dp]},
{s[" θ'τ*rgy"], " = ", s[n0[Θ'[T] Sqrt[яi[T]^2+Z[T]^2]]], s["mc"], s[dp]},
{s[" E kinet"], " = ", s[n0[ekin[T]]], s["mc²"], s[dp]},
{s[" E poten"], " = ", s[n0[epot[T]]], s["mc²"], s[dp]},
{s[" E tot-m"], " = ", s[n0[ε-1]], s["mc²"], s[dp]},
{s[" CarterQ"], " = ", s[N[Q]], s["GMm/c"], s[dp]},
{s[" L axial"], " = ", s[n0[Lz]], s["GMm/c"], s[dp]},
{s[" L polar"], " = ", s[n0[pΘ[T]]], s["GMm/c"], s[dp]},
{s[" p r.mom"], " = ", s[n0[pR[T]]], s["mc"], s[dp]},
{s[" R carts"], " = ", s[n0[XYZ[T]]], s["GM/c²"], s[dp]},
{s[" x carts"], " = ", s[n0[X[T]]], s["GM/c²"], s[dp]},
{s[" y carts"], " = ", s[n0[Y[T]]], s["GM/c²"], s[dp]},
{s[" z carts"], " = ", s[n0[Z[T]]], s["GM/c²"], s[dp]},
{s[" ω fdrag"], " = ", s[n0[ω[T]]], s["c³/G/M"], s[dp]},
{s[" v fdrag"], " = ", s[n0[й[T]]], s["c"], s[dp]},
{s[" Ω fdrag"], " = ", s[n0[Ω[T]]], s["c"], s[dp]},
{s[" v obsvd"], " = ", s[n0[ß[T]]], s["c"], s[dp]},
{s[" v escpe"], " = ", s[n0[ж[T]]], s["c"], s[dp]},
{s[" v delay"], " = ", s[n0[sh[T]]], s["c"], s[dp]},
{s[" v local"], " = ", s[n0[v[T]]], s["c"], s[dp]},
{s[" "], s[" "], s["                   "], s["         "]}},
Alignment-> Left, Spacings-> {0, 0}];

PR=1.2r0;                                                                   (* Plot Range *)
VP={r0, r0, r0};                                                      (* Perspektive x,y,z*)
d1=50;                                                                    (* Schweiflänge *)
mrec=10;                                                 (* Parametric Plot Subdivisionen *)
imgsize=380;                                                                 (* Bildgröße *)

s[text_]:=Style[text, FontSize->font]; font=11;                            (* Anzeigestil *)

A=a;                                   (* pseudosphärisch [BL]: A=0, kartesisch [KS]: A=a *)

plot0[{xx_, yy_, zz_, tk_}]:=
Rasterize[
Show[Graphics3D[{
{PointSize[0.007], Red, Point[{X[T], Y[T], Z[T]}]}},
ImageSize-> imgsize,
PlotRange-> PR,
SphericalRegion->False,
ImagePadding-> 1],
horizons[A, None],
ViewPoint-> {xx, yy, zz}]];

plot1[{xx_, yy_, zz_, tk_}]:=
Rasterize[
Show[Graphics3D[{
{PointSize[0.007], Red, Point[{X[T], Y[T], Z[T]}]}},
ImageSize-> imgsize,
PlotRange-> PR,
SphericalRegion->False,
ImagePadding-> 1],
horizons[A, None],
Graphics3D[{{PointSize[0.012], Blue, Point[
{Sin[-щ tk+π/2] Sqrt[X[0]^2+Y[0]^2], Cos[-щ tk+π/2] Sqrt[X[0]^2+Y[0]^2], Z[0]}]}}],
ParametricPlot3D[{X[tt], Y[tt], Z[tt]}, {tt, 0, Max[1*^-16, T-d1/3]},
PlotStyle-> {Thickness[0.003], Gray},
PlotPoints-> Automatic,
MaxRecursion-> mrec],
ParametricPlot3D[{X[tt], Y[tt], Z[tt]}, {tt, Max[0, T-d1], T},
PlotStyle-> {Thickness[0.004]},
ColorFunction-> Function[{x, y, z, t},
Hue[0, 1, 0.5, Max[Min[(-T+(t+d1))/d1, 1], 0]]],
ColorFunctionScaling-> False,
PlotPoints-> Automatic,
MaxRecursion-> mrec],
ViewPoint-> {xx, yy, zz}]];

Do[
Print[Rasterize[Grid[{{
plot0[{0, -Infinity, 0, tk}], plot0[{0, 0, Infinity, tk}], display[Quiet[д[tk]]]
}}, Alignment->Left]]],
{tk, 0, 0, 1}]

Do[
Print[Rasterize[Grid[{{
plot1[{0, -Infinity, 0, tk}], plot1[{0, 0, Infinity, tk}], display[Quiet[д[tk]]]
}}, Alignment->Left]]],
{tk, Tmax, Tmax, 10}]

(* http://kerr.yukerez.net *) (* Code by Simon Tyran, Vienna *)

[JuRo]

Hula, wie blöde bist du denn noch, was willst du mit diesen halben Märchen

Der Lichtstrahl bewegt sich bei dir laut SRT nun auf der Y-Achse bzw. H-Achse (System k)

Was sehen wir und was sehen deine Notare für eine Geschwindigkeit für den Lichtstrahl auf beiden Achsen

[Yukterez]

Was willst du mit Sqrt[1 - v^2/c^2], wir haben keine bewegten Bezugssysteme?

Na, du vollgekoteter Alkoholiker? Bist du schon wieder in deinem eigenen Erbrochenen aufgewacht?

Einen guten Morgen wünschend,