julian apostata hat geschrieben:
- deltavbremse2hm3.jpg (23.56 KiB) 7678-mal betrachtet
@Lothar
Δv=f(x)
Wie lautet denn nun f(x) überhaupt? Oder fangen wir mal ganz weit unten an. Wie hast du Δv überhaupt definiert?
Also ich würde folgende Möglichkeiten in betracht ziehen: Δv=v1-v2
Sinnvoll wäre vielleicht auch Δv=(v1-v2)/d , also Lichtwindigkeitsdifferenz pro Meter?
Oder definierst du es ganz anders?
Gut, das klingt jetzt schon wesentlich besser und intelligenter als seine rotzfreche Bewertung „alles völlig wertloses blabla“ und „Pseudoerklärung“ von zuletzt. Es ist ihm also inzwischen ein Licht aufgegangen.
Was er da als Definition von Δv in Betracht zieht, ist schon mal ein guter Anfang. Ich würde es auch nicht anders definieren. Und seine Überlegung zeigt, daß er den Sachverhalt wohl begriffen hat. Gratulation.
Selbstverständlich ist hier eine Geschwindigkeitsdifferenz Δv immer bezogen auf zwei Punkte des Lichtstrahls, egal wie groß die Strecke a zwischen den beiden Punkten ist, ob eine Wellenlänge (a=λ), oder die Länge a=c*T eines Lichtpulses der Dauer T, oder die Länge a=c*T des Lichtstrahls vom Aufleuchten bis zum Erlöschen einer Supernova mit der Leuchtdauer T. Es gilt also richtig Δv(a)=v1-v2
Und selbstverständlich gilt richtig für die Geschwindigkeitsdifferenz je Meter Länge für jede beliebige Zwischenlänge (z.B.Wellenlänge λ) zwischen diesen beiden Punkten des Lichtstrahls die Formel Δv/m=(v1-v2)/a.
Für eine beliebige Welle der Länge λ in diesem Lichtstrahl ergibt sich also die zugehörige Geschwindigkeitsdifferenz zu
Δv(λ)=(v1-v2)/a * λ
Vergrößert sich infolge Δv(a) im Laufe der Laufzeit D der Abstand a zwischen den beiden Punkten, z.B. der Abstand a zwischen dem Aufleuchtepunkt und dem Erlöschungspunkt des Lichtstrahls bei einer Supernova, um Δv(a)*D=(v1-v2)*D, vergrößert sich der Abstand des Wellenanfangs vom Wellenende einer Welle der Länge λ innerhalb dieses Lichtstrahls um Δλ = Δv(λ )*D=(v1-v2)/a* λ *D
Es gilt also für das Verhältnis
Verlängerung der Leuchtdauer Δv(a)*D / Wellenverlängerung Δv(λ )*D =
= (v1-v2)*D /[(v1-v2)/a* λ *D] =
= a / λ
Das heißt, Verlängerung der Leuchtdauer und Wellenverlängerung verhalten sich in jeder beliebigen Laufzeit-Entfernung D wie ursprünglicher Leuchtdauer-Abstand a zur ursprünglichen Wellenlänge λ.
Verdoppelt sich also der Abstand a zwischen dem Aufleuchtepunkt und dem Erlöschungspunkt des Lichtstrahls bei einer Supernova, verdoppelt sich also die scheinbare Leuchtdauer der Supernova, verdoppeln sich die Längen aller Wellen der Länge λ in diesem Lichtstrahl ebenfalls auf das Doppelte.
Die Rotverschiebung einer Supernova durch Wellenverlängerung (infolge eines Δv durch die Explosion) korreliert also ganz exakt mit der Leuchtdauer einer Supernova.
Hierbei ist es völlig unerheblich, wie die Funktion Δv = f(x) aussieht, wie schnell oder langsam also Δv im Laufe der Laufzeit abnimmt.
Wie ersichtlich, läßt sich die Rotverschiebung der Supernovae und die mit ihr korrelierende Verlängerung der Leuchtdauer mit einfachster klassischer Physik, klassischer Geschwindigkeitsaddition und einfachster Mathematik qualitativ und quantitativ erfassen. Demgegenüber ist die relativistische Erklärung mit invarianter Lichtgeschwindigkeit und Expansion des Raumes und Mitnahme der Galaxien mit Überlichtgeschwindigkeit als absoluter Schwachsinn erkennbar.
Mit freundlichen Grüßen
Lothar Pernes
, 
hat geschrieben:Wie berechnest du z mit v=2,09 c?
, 
hat geschrieben:Wie berechnest du z mit v=2,09 c?
hat geschrieben:2.09 c zum Zeitpunkt der Emssion oder der Absorption?
, 
, 
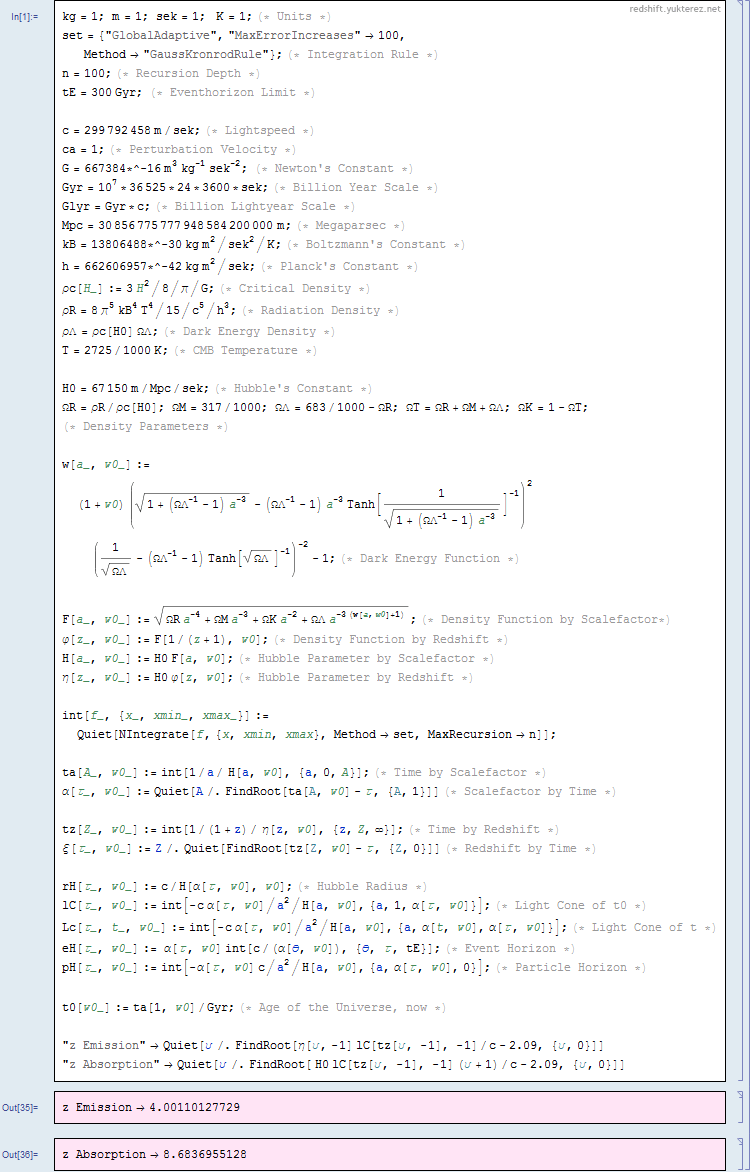
hat geschrieben:Du kannst also nicht rechnen! :sabber: :lol:
, 