Hallo Forum
Hier möchte ich darlegen, weshalb in der IEEE 754 Norm äußerst sinnvolle Dinge definiert werden, die bisher jeder Mathematiker als Unsinn bezeichnen würde. Die Grundlagen dafür stammen aber nicht, wie man vermuten könnte, speziell aus dem Bereich der binären Aritmetik (Computer) sondern waren einst auch Grundsatzüberlegungen darüber, wie man mit besonderen Rechenaufgaben umgeht, insbesondere, wenn sie eine 0 enthalten, ganz besonders im Nenner. Leider finde ich im Netz keinerlei Referenzen darüber, die ich verlinken könnte, aber solche sind hoffentlich auch nicht nötig, wenn die Argumente für sich selber sprechen. Man muss sich aber von vorne herein klar machen, dass das Folgende zwar in der IEEE 754 Verwendung findet, jedoch auch überall gilt (bis auf den "Blödsinn" am Schluß, den man tatsächlich nur für Computer erdacht hat.)
Das Unheil nimmt seinen Lauf bei der Frage, was 1/0 sein könnte, lt. Wikipedia soll es undefiniert sein und als Argument wird neben dem Beweis über den algebraischen Ring auch erwähnt, dass 1/0 nicht unendlich sein kann, weil 0*unendlich auch nicht 1 ist. Was aber genau ist 0*unendlich oder überhaupt kann im Umkehrschluß 0*x stets 0 ergeben, wo doch 0/0 sicher nicht mehr x sondern undefiniert ergibt? Gibt es etwa doch ein Element a≠0 für welches 0*x=a gilt? Natürlich gäbe es eines, bzw. derer gleich drei, wenn man den Definitionsbereich der reellen Zahlen verlässt und nur noch von Tendenzen redet. Für den Beweis von 1/0=undefiniert wäre das das Aus und das andere Argument wurde bereits mit 0/0≠x ausgehebelt. Die drei Elemente wären
1/0=unendlich (Tendez zu höchsten Werten, sicher > 0),
0/0=nicht definiert (Tendenz zur 0, aber sicher keineswegs 0) und
-1/0=-unendlich (Tendenz zu niedrigsten Werten, sicher < 0)
wie sie in der IEEE 754 definiert sind. Nun braucht man x/0 eigentlich nur noch in x*(1/0) umzuformen, was mathematisch noch vollkommen korrekt ist und schon reduziert sich das Ganze auf x*unendlich. Ist x nun 0 steht dort 0*1/0 und nur das ist undefiniert. Ist x hingegen ungleich 0 reicht das Vorzeichen bzw. das Signum von x (-1 bei x<0 und 1 bei x>0) um die Tendenzen unendlich oder -unendlich als Ergebnis zu erhalten. Alles in allem sieht das so aus
x*unendlich=undefiniert für x=0 und x=undefiniert,
x*unendlich=unendlich für x>0 inkl. unendlich und
x*unendlich=-unendlich für x<0 inklusive -unendlich
sowie
x*-unendlich=undefiniert für x=0 und x=undefiniert,
x*-unendlich=-unendlich für x>0 inkl. unendlich und
x*-unendlich=unendlich für x<0 inklusive -unendlich
Da sich Faktoren in der Reihenfolge beliebig verändern dürfen, egibt sich daraus x*undefiniert=undefiniert in jedem Fall, also auch bei 0*undefiniert. 0*x für x=Tendenz ist also keinesfalls 0.
Mit diesen Tendenzen kann man aber nicht bloß multiplizieren, sondern auch dividieren, addieren und subtrahieren. Für die Division x/Tendenz sind diese sogar recht einfach, denn teilt man durch nicht definiert stehen sowohl in Zähler als auch im Nenner jeweils eine 0, so dass das Ergebnis nur noch nicht definiert sein kann. Andernfalls ist das Ergebnis 0 wenn x≠Tendenz und undefiniert wenn x=Tendenz ist. Für Addition und Subtraktion gelten schließlich folgende Regeln
x±undefinier=undefiniert±x=undefiniert für alle x
x-unendlich=x+(-unendlich)=-unendlich für alle x≠Tendenz
x+unendlich=x-(-unendlich)=unendlich für alle x≠Tendenz
x-unendlich=x+(-unendlich)=undefiniert für alle x=Tendenz
x+unendlich=x-(-unendlich)=undefiniert für alle x=Tendenz
Zum guten Schluß wäre da noch - und das tatsächlich nur im Computer - undefiniert≠undefiniert, damit man mit if(a≠a) auf undefiniert testen kann und die -0, die signalisiert, dass die Vorzeichen einer Multiplikation und/oder einer Division unterschiedlich waren. In der allgemeinen Mathematik gäbe es dafür im Gegensatz zum Rest jedenfalls keine Verwendung.
Die Magie der 0
2 Beiträge • Seite 1 von 1
Re: Die Magie der 0
Hehehe...
Habe gerade etwas über Peano-Axiome gelesen, man lernt ja nie aus. Da dachte ich mir, evtl. sollte es auch Pohlsche Axiome geben:
1. Jede Zahl n verursacht durch Addition oder Subtraktion eine Änderung von Summen und Differenzen, die 0 tut dies nicht.
2. Die 0 ist deswegen keine Zahl, sondern neben ,
, 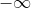 und
und 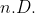 einer von 4 Indikatoren, die wie folgt definiert sind:
einer von 4 Indikatoren, die wie folgt definiert sind:
2a. 0=0
2b. 0/0=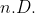
2c. 1/0=
2d. -1/0=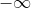
3. Für alle Elemente dieser Gruppe, bis auf=-\infty+\infty=NaN) gilt, dass sie das Ergebnis von Summen und Differenzen nicht verändern.
gilt, dass sie das Ergebnis von Summen und Differenzen nicht verändern.
4. Multiplikationen von Zahlen mit Indikatoren ergeben im Produkt einen Indikator.
5. Subtraktionen sind Additionen bei denen das Vorzeichen des zweiten Summanden verändert wird (z.B. 1-(+1)=1+(-1)).
6. Divisionen sind Multiplikationen mit der ersten natürlichen Zahl geteilt durch den Divisor (Kehrwertbildung; a/b=a*(1/b)).
7. Für die 4 Elemente der Zahlengruppe der Indikatoren gelten folgende Größenordnungen:
7a.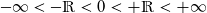
7b.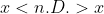 für alle x inklusive Indikatoren - insbesondere auch
für alle x inklusive Indikatoren - insbesondere auch 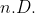 selbst.
selbst.
7c.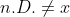 für alle x inklusive Indikatoren - insbesondere auch
für alle x inklusive Indikatoren - insbesondere auch 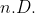 selbst.
selbst.
Man wird feststellen, dass diese Regeln die Peano-Axiome bis auf kleine Änderungen, die nur die 0 betreffen, beinhalten. Die neue Zahlengruppe sollte noch einen Buchstaben erhalten, wofür ich P vorschlage, sofern er noch frei ist und die Zahlengruppe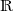 erweitern.
erweitern.
Habe gerade etwas über Peano-Axiome gelesen, man lernt ja nie aus. Da dachte ich mir, evtl. sollte es auch Pohlsche Axiome geben:
1. Jede Zahl n verursacht durch Addition oder Subtraktion eine Änderung von Summen und Differenzen, die 0 tut dies nicht.
2. Die 0 ist deswegen keine Zahl, sondern neben
2a. 0=0
2b. 0/0=
2c. 1/0=
2d. -1/0=
3. Für alle Elemente dieser Gruppe, bis auf
4. Multiplikationen von Zahlen mit Indikatoren ergeben im Produkt einen Indikator.
5. Subtraktionen sind Additionen bei denen das Vorzeichen des zweiten Summanden verändert wird (z.B. 1-(+1)=1+(-1)).
6. Divisionen sind Multiplikationen mit der ersten natürlichen Zahl geteilt durch den Divisor (Kehrwertbildung; a/b=a*(1/b)).
7. Für die 4 Elemente der Zahlengruppe der Indikatoren gelten folgende Größenordnungen:
7a.
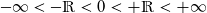
7b.
7c.
Man wird feststellen, dass diese Regeln die Peano-Axiome bis auf kleine Änderungen, die nur die 0 betreffen, beinhalten. Die neue Zahlengruppe sollte noch einen Buchstaben erhalten, wofür ich P vorschlage, sofern er noch frei ist und die Zahlengruppe
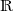 erweitern.
erweitern.- Nicht von Bedeutung
2 Beiträge • Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 5 Gäste
